Minnesota's new flag: from scratch

A new flag

Minnesota is soon getting a new state flag.

In May 2023, the Minnesota Legislature passed, and the governor signed, HF 1830, a state government finance bill that also created a commission to redesign Minnesota's state flag and state seal. The previous flag design uses the classic "seal on a bedsheet" arrangement decried by vexillologists.¹ Seals and flags have opposite purposes: seals are supposed to be complicated while flags are supposed to be simple and recognizable from a distance.²

In the second half of 2023, the State Emblems Redesign Commission invited members of the public to submit proposed designs for Minnesota's new flag and seal. Many designs were proposed. The winning proposal was proposal F1953, designed and submitted by Andrew Prekker of Luverne, Minnesota. The commission adopted a simplified version of Prekker's design this past December. This design will be adopted on May 11, the 166th anniversary of Minnesota statehood. The new design is thought to be one of the best in the nation.

In this post, I will explain how to implement the design of this flag as a short manually-coded SVG file.

The specifications

The new flag as a very simple design, specified by the State Emblems Redesign Commission in its official report (p. 21). You can make the flag out of three shapes:

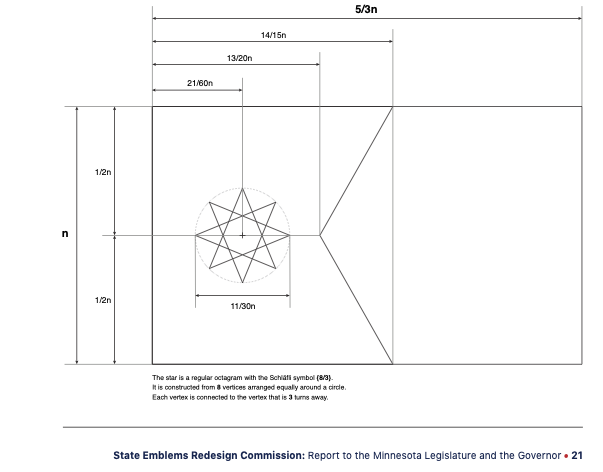
• A water blue (#52c9e8) rectangle. Two sides of the rectangle have length \(n\) and the other two sides have length \(5n/3\).

• A night sky blue (#002d5d) pentagon with three sides lying on the edges of the rectangle: one side that is the entire edge of the rectangle with length \(n\), and the two neighboring perpendicular sides that have a length of \(14n/15\). The last two sides meet at a vertex halfway between the long edges of the rectangle and a distance \(13n/20\) away from the opposite edge of the pentagon.

  

• A white eight-pointed star, which is a regular octogram. The center of the star is halfway between the long edges of the rectangle, and a distance of \(21n/60\) from the short edge of the rectangle that is also an edge of the pentagon. The points of the star are eight evenly spaced points along a circle of radius \(11n/60\), with two points on a line perpendicular to the long sides of the rectangle and two points on a line perpendicular to the short sides. An outline of this polygon can be constructed by connecting each of these eight points with the points three away.

  

  

Coding the flag

We can use these descriptions to write our SVG file.

Outside element

We begin with the outside svg element, which defines the viewport. Since the flag sits inside of a \(n \times 5n/3\) rectangle, we'll set \(n = 300\), so that the flag's dimensions are 500 × 300.

Typically, in computer graphics, the \(y\) coordinates increase as you go down, which is the opposite of the convention used in mathematics. So, our viewport's upper-left corner will be at \((0, 0)\), and the lower right corner will be at \((500, 300)\). This is expressed in SVG with the attribute viewbox="0 0 500 300" in the svg element.

<svg viewbox="0 0 500 300" xmlns='http://www.w3.org/2000/svg'>
</svg>

Water blue rectangle

The next element to add is a water blue (#52c9e8) rectangle with the same dimensions as the viewport. We'll use the rect element for this. We insert the rect inside the svg element.

<svg viewbox="0 0 500 300" xmlns='http://www.w3.org/2000/svg'>
  <rect x="0" y="0" width="500" height="300" stroke="none" fill="#52c9e8" />
</svg>

Night sky blue pentagon

The next element to add is the night-sky blue (#002d5d) pentagon. For this, we'll use the polygon element.³ Setting \(n = 300\), we see that the points of the vertices of the pentagon are at the following coordinates: \[(0, 0), (280, 0), (195, 150), (280, 300), (0, 300).\] So, we insert after the rect:

  <polygon points="0,0 280,0 195,150 280,300 0,300"
    stroke="none" fill="#002d5d" />

White star

Last, and most tricky, is the eight-pointed star that goes inside the pentagon. To get these points, we are going to use some trigonometry. If a circle has radius \(r\) and center at the origin, then each point \(P\) on the circle has the form \[P = (r \cos \theta, r \sin \theta),\] where \(\theta\) is the angle between the positive \(x\)-axis and the ray starting at the center of the circle and passing through \(P\). For a circle with arbitrary center \((h, k),\) we translate to get the parameterization \[P = (h + r \cos \theta, k + r \sin \theta).\]

In our case, the points of the star sit on a circle with center \(105, 150)\) and radius 55. There are eight points equally spaced around the circle, with two points on the same horizontal line as the center, so the appropriate angles are 0°, 45°, 90°, 135°, and so on—or, in radians, \(0, \pi/4, \pi/2, 3\pi/4, \dots\). However, we create the star by attaching each point to a point three away, so the first point has an angle of \(0\), the next an angle of \(3\pi/4\), the next an angle of \(3\pi/2\), etc. Specifically, the \(j\)th point will have an angle of \(3j\pi/4\), and so the \(j\)th point will have coordinates \[(105 + 55 \cos(3j\pi/4), 150 + 55 \sin(3j\pi/4)).\]

We could compute these by hand (using knowledge of trigonometry and a decimal approximation for \(\sqrt{2}/2\)), but a short Python script is perfect for this.

"""Calculate the points of the star on the Minnesota flag"""
import math

center_x = 105
center_y = 150
r = 55

theta = [3 * k * math.pi / 4 for k in range(0, 9)]
p = [(center_x + r * math.cos(k), center_y + r * math.sin(k)) for k in theta]

for pt in p:
    print(f"{pt[0]:08.8f},{pt[1]:08.8f}")

We run this script to get the coordinates:

python3 star_points.py

160.00000000,150.00000000
66.10912703,188.89087297
105.00000000,95.00000000
143.89087297,188.89087297
50.00000000,150.00000000
143.89087297,111.10912703
105.00000000,205.00000000
66.10912703,111.10912703
160.00000000,150.00000000

Now, we use the polyline SVG element, inserting the following after the pentagon in our SVG file:

  <polyline points="
    160.00000000,150.00000000
    66.10912703,188.89087297
    105.00000000,95.00000000
    143.89087297,188.89087297
    50.00000000,150.00000000
    143.89087297,111.10912703
    105.00000000,205.00000000
    66.10912703,111.10912703
    160.00000000,150.00000000"
    stroke="none" fill="white" />

Final result

The final result is this short SVG file:

<svg viewbox="0 0 500 300" xmlns='http://www.w3.org/2000/svg'>
  <rect x="0" y="0" width="500" height="300" stroke="none" fill="#52c9e8" />
  <polygon points="0,0 280,0 195,150 280,300 0,300"
    stroke="none" fill="#002d5d" />
  <polyline points="
    160.00000000,150.00000000
    66.10912703,188.89087297
    105.00000000,95.00000000
    143.89087297,188.89087297
    50.00000000,150.00000000
    143.89087297,111.10912703
    105.00000000,205.00000000
    66.10912703,111.10912703
    160.00000000,150.00000000"
    stroke="none" fill="white" />
</svg>

And it looks like this:

What a beautiful flag!

Footnotes