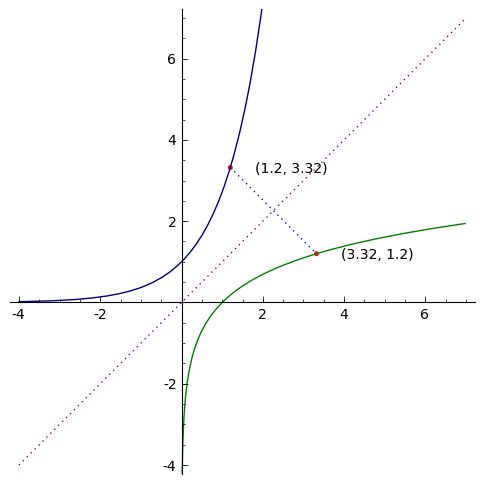
Suppose f is a one-to-one function. For every point P1=(a,b)
on the graph of y=f(x), there is a corresponding point P2=(b,a) on the
graph of y=f−1(x) . The points P1 and P2 are reflections of each other
over the line y=x. In the illustration below, a=1.2 and b=3.32.
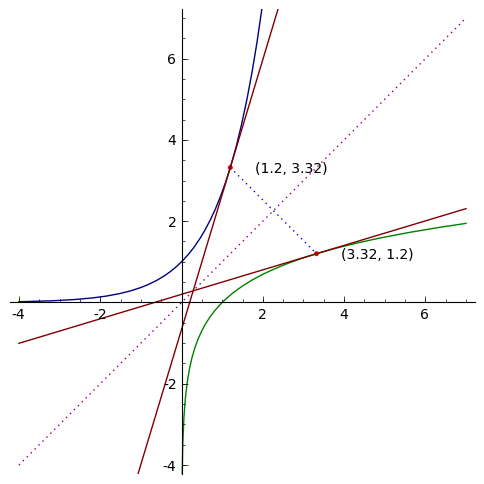
 Now, suppose we have a line tangent to y=f(x) at the point (a,b). The
Now, suppose we have a line tangent to y=f(x) at the point (a,b). The
slope m of this line will be m=f′(a). Since the graph of y=f−1(x) is
the reflection of the graph of y=f(x), the line tangent to y=f−1(x)
at (b,a) will have a slope of 1/m , the reciprocal of m.
 Here is an animation showing the two tangent lines at various values of a:
Here is an animation showing the two tangent lines at various values of a:
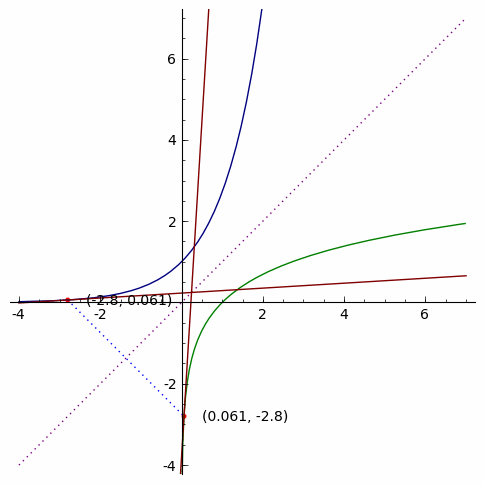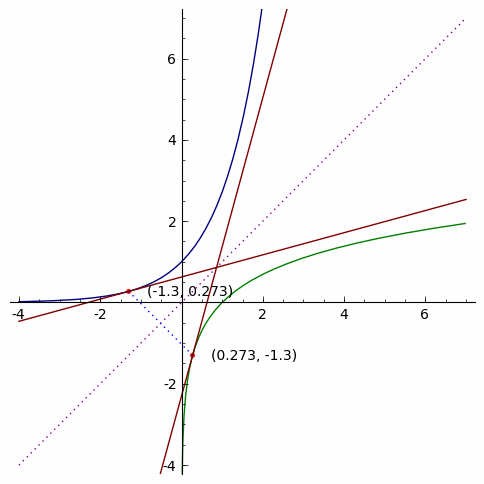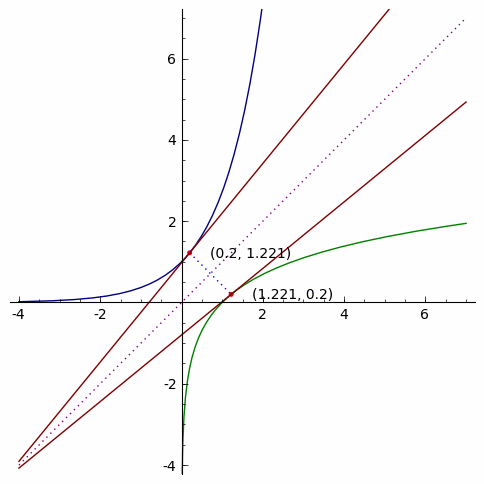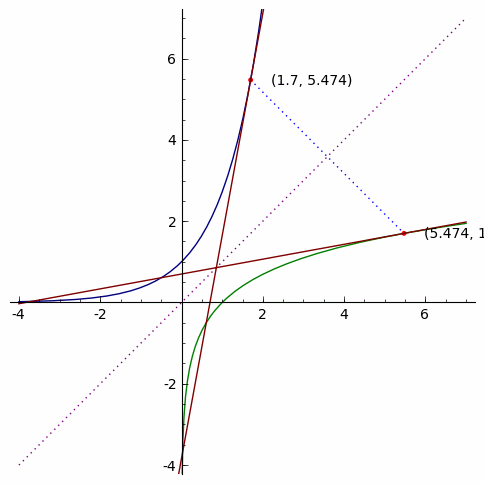
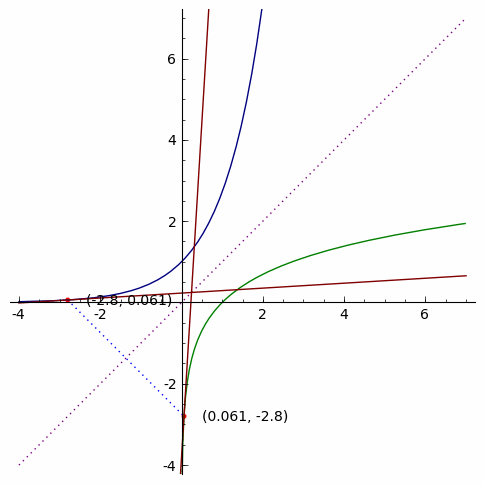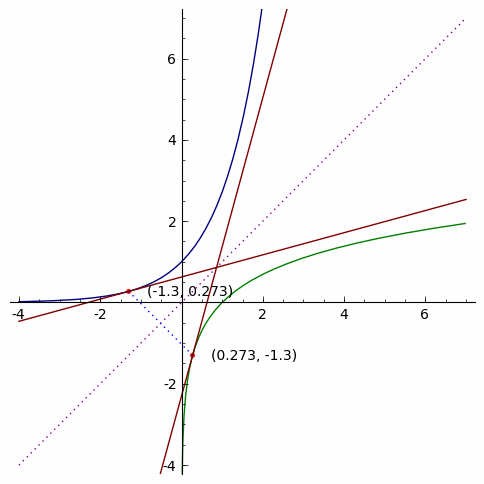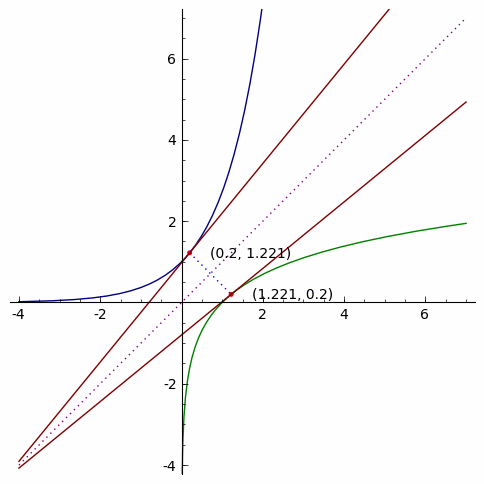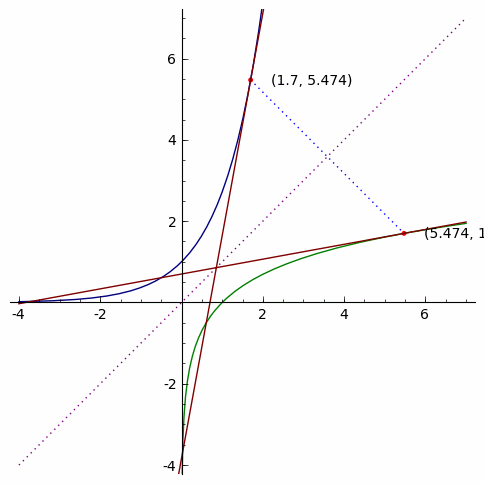
.gif)
.gif)